Chủ đề học tập : Tứ giác nội tiếp đường tròn
Tứ giác nội tiếp là phần kiến thức quan trọng trong chương trình toán lớp 9. Dưới đây Takis sẽ tổng hợp các kiến thức trọng tâm và các dạng bài tập có liên quan ở nội dung này.
I. Lý thuyết
1. Khái niệm về tứ giác nội tiếp
Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).

2. Định lí
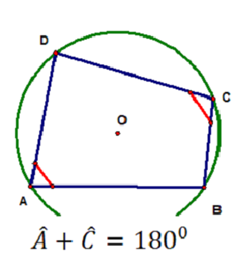
Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.
Ví dụ 3. Cho tứ giác ABCD nội tiếp đường tròn (O).


Chú ý:
1.Trong các hình đã học thì hình chữ nhật, hình vuông, hình thang cân nội tiếp được đường tròn.
2.Góc nội tiếp chắn nửa đường tròn đường kính thì có số đo bằng 900
3.Đường kính đi qua trung điểm của dây thì vuông góc với dây
4.Nếu hai tiếp tuyến cắt nhau tại một điểm thì:
+ Điểm đó cách đều hai tiếp điểm
+ Đường thẳng nối từ điểm đó đến tâm là phân giác của góc tạo bởi hai tiếp tuyến
+ Đường thẳng nối từ tâm đến điểm đó là phân giác của góc tạo bởi hai bán kính qua tiếp điểm.
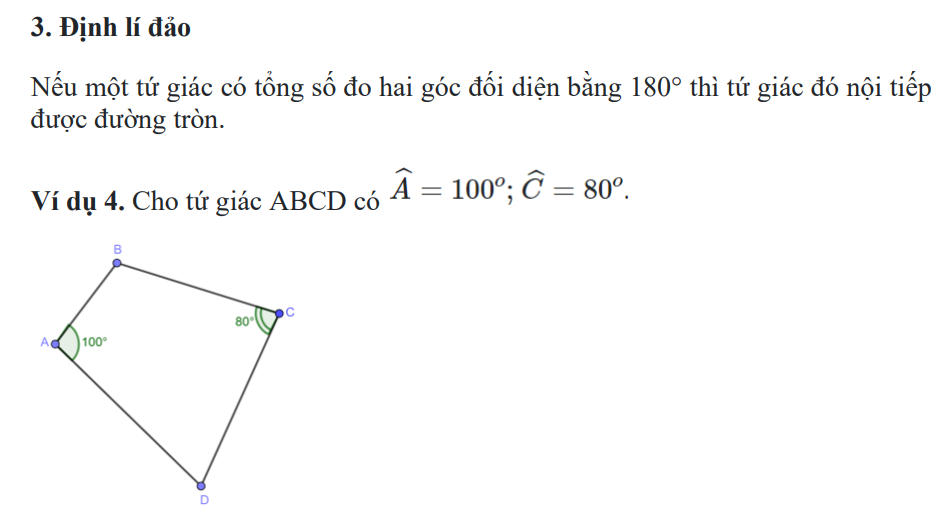
Ví dụ 5. Tứ giác ABCD có , góc ngoài của tam giác tại đỉnh A có số đo bằng 80o.
+ ˆAA^ và ˆCC^ là hai góc đối diện.
+ Góc ngoài đỉnh A và góc trong đỉnh C có tổng số đo bằng 180o.
Do đó tứ giác ABCD nội tiếp đường tròn.
II. Các dạng bài tập
Dạng 1. Chứng minh tứ giác nội tiếp
Phương pháp giải: Để chứng minh tứ giác nội tiếp, ta có thể sử dụng một trong các cách sau:
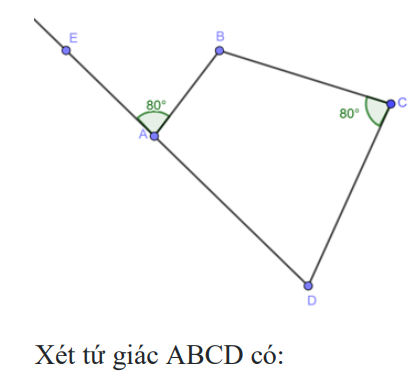
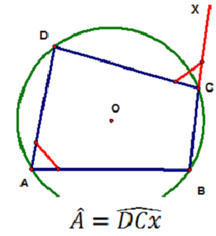
Phương pháp 1: Chứng minh tứ giác có tổng hai góc đối bằng 180
Minh họa:
Phương pháp 2: Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó thì nội tiếp được trong một đường tròn
Minh họa:
Phương pháp 3: Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau
Minh họa:

Phương pháp 4: Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó
Minh họa:
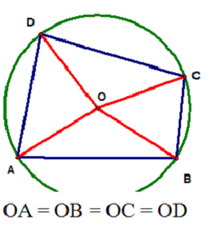
Bài 1: Cho tam giác ABC, 2 đường cao BB’, CC’. Chứng minh tứ giác BCB’C’ nội tiếp.
Hướng Dẫn:
Cách 1: Phương pháp 2:Chứng minh 4 đỉnh cách đều 1 điểm
OB’ là đường trung tuyến ứng với cạnh huyền

Cách 2: Phương pháp 3:Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lạ dưới một góc bằng nhau là tứ giác nội tiếp.

Cách 3: Phương pháp 1 và phương pháp 4: Tứ giác có tổng 2 góc đối bằng và Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

Bài 2: Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiêp.
Hướng Dẫn:
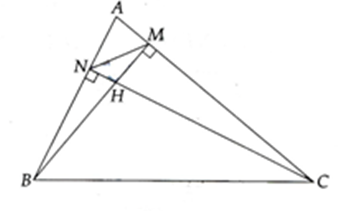

Dạng 2. Sử dụng tứ giác nội tiếp để chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau, các đường thẳng song song hoặc đồng quy, các tam giác đồng dạng...
Phương pháp: Sử dụng tính chât của tứ giác nội tiếp.
Bài 1: Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E, kẻ CK ^ AE tại K. Đường thẳng DE cắt CK tại F. Chứng minh:
a) Tứ giác AHCK là tứ giác nội tiếp;
b) AH.AB = AD2;
c) Tam giác ACE là tam giác cân.
Hướng Dẫn:
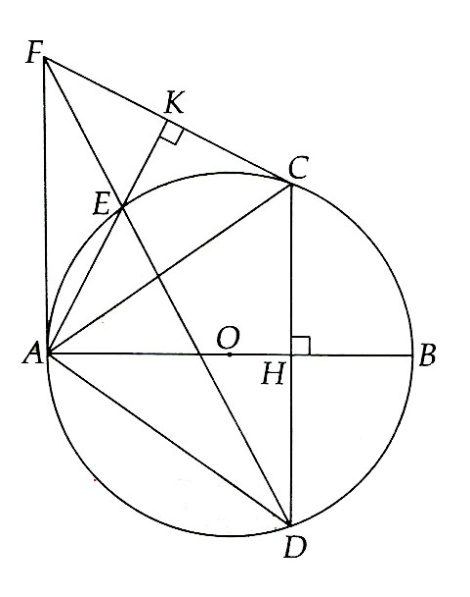
a) Học sinh tự chứng minh
b) DADB vuông tại D, có đường cao DH Þ AD2 = AH.AB

Bài 2: Cho nửa (O) đường kính AB. Lấy M Î OA (M không trùng o và A). Qua M vẽ đường thẳng d vuông góc với AB. Trên d lấy N sao cho ON > R. Nôi NB cắt (O) tại c. Kẻ tiếp tuyến NE với (O) (£ là tiếp điểm, E và A cùng thuộc nửa mặt phẳng bờ d). Chứng minh:
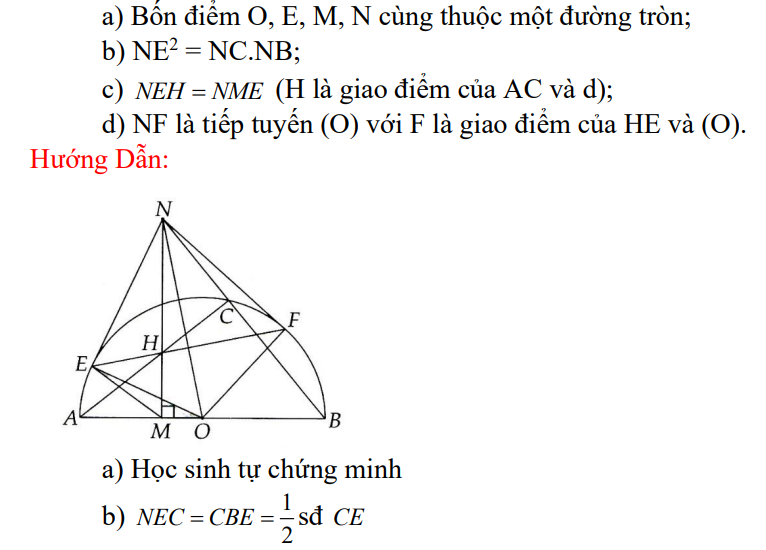

Dạng 3: Chứng minh các điểm cùng thuộc một đường tròn
Phương pháp: Chỉ ra khoảng cách từ một điểm tới tất cả các điểm đều bằng nhau.
Lợi dụng các tam giác vuông có cạnh huyền chung
Chứng minh các đỉnh của một đa giác cùng nằm trên một đường tròn.
Sử dụng cung chứa góc.
Chứng minh các tứ giác nội tiếp.
Bài 1:Cho hình thoi ABCD có góc A bằng , AB = a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn. Xác định tâm và tính bán kính của đường tròn đó theo a.
Hướng Dẫn:
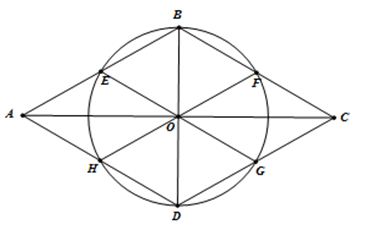
Gọi O là giao điểm của AC và BD ta có OB = OD
Do ABCD là hình thoi nên ta có:


Trên đây là nội dung và một số dạng bài tập cơ bản về chủ đề Tứ giác nội tiếp đường tròn. Hãy theo dõi ngay tại takis.vn để có thêm nhiều kiến thức mới và hay 3 môn Toán Anh Văn nhé!
1. Khái niệm về tứ giác nội tiếp
Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp).

2. Định lí
Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.
Ví dụ 3. Cho tứ giác ABCD nội tiếp đường tròn (O).



Chú ý:
1.Trong các hình đã học thì hình chữ nhật, hình vuông, hình thang cân nội tiếp được đường tròn.
2.Góc nội tiếp chắn nửa đường tròn đường kính thì có số đo bằng 900
3.Đường kính đi qua trung điểm của dây thì vuông góc với dây
4.Nếu hai tiếp tuyến cắt nhau tại một điểm thì:
+ Điểm đó cách đều hai tiếp điểm
+ Đường thẳng nối từ điểm đó đến tâm là phân giác của góc tạo bởi hai tiếp tuyến
+ Đường thẳng nối từ tâm đến điểm đó là phân giác của góc tạo bởi hai bán kính qua tiếp điểm.
Ví dụ 5. Tứ giác ABCD có , góc ngoài của tam giác tại đỉnh A có số đo bằng 80o.

+ ˆAA^ và ˆCC^ là hai góc đối diện.
+ Góc ngoài đỉnh A và góc trong đỉnh C có tổng số đo bằng 180o.
Do đó tứ giác ABCD nội tiếp đường tròn.
II. Các dạng bài tập
Dạng 1. Chứng minh tứ giác nội tiếp
Phương pháp giải: Để chứng minh tứ giác nội tiếp, ta có thể sử dụng một trong các cách sau:
Phương pháp 1: Chứng minh tứ giác có tổng hai góc đối bằng 180
Minh họa:

Phương pháp 2: Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó thì nội tiếp được trong một đường tròn
Minh họa:

Phương pháp 3: Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau
Minh họa:

Phương pháp 4: Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó
Minh họa:

Bài 1: Cho tam giác ABC, 2 đường cao BB’, CC’. Chứng minh tứ giác BCB’C’ nội tiếp.
Hướng Dẫn:
Cách 1: Phương pháp 2:Chứng minh 4 đỉnh cách đều 1 điểm
OB’ là đường trung tuyến ứng với cạnh huyền

Cách 2: Phương pháp 3:Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lạ dưới một góc bằng nhau là tứ giác nội tiếp.

Cách 3: Phương pháp 1 và phương pháp 4: Tứ giác có tổng 2 góc đối bằng và Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

Bài 2: Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là những tứ giác nội tiêp.
Hướng Dẫn:


Dạng 2. Sử dụng tứ giác nội tiếp để chứng minh các góc bằng nhau, các đoạn thẳng bằng nhau, các đường thẳng song song hoặc đồng quy, các tam giác đồng dạng...
Phương pháp: Sử dụng tính chât của tứ giác nội tiếp.
Bài 1: Cho đường tròn (O) đường kính AB. Gọi H là điểm nằm giữa O và B. Kẻ dây CD vuông góc với AB tại H. Trên cung nhỏ AC lấy điểm E, kẻ CK ^ AE tại K. Đường thẳng DE cắt CK tại F. Chứng minh:
a) Tứ giác AHCK là tứ giác nội tiếp;
b) AH.AB = AD2;
c) Tam giác ACE là tam giác cân.
Hướng Dẫn:

a) Học sinh tự chứng minh
b) DADB vuông tại D, có đường cao DH Þ AD2 = AH.AB

Bài 2: Cho nửa (O) đường kính AB. Lấy M Î OA (M không trùng o và A). Qua M vẽ đường thẳng d vuông góc với AB. Trên d lấy N sao cho ON > R. Nôi NB cắt (O) tại c. Kẻ tiếp tuyến NE với (O) (£ là tiếp điểm, E và A cùng thuộc nửa mặt phẳng bờ d). Chứng minh:


Dạng 3: Chứng minh các điểm cùng thuộc một đường tròn
Phương pháp: Chỉ ra khoảng cách từ một điểm tới tất cả các điểm đều bằng nhau.
Lợi dụng các tam giác vuông có cạnh huyền chung
Chứng minh các đỉnh của một đa giác cùng nằm trên một đường tròn.
Sử dụng cung chứa góc.
Chứng minh các tứ giác nội tiếp.
Bài 1:Cho hình thoi ABCD có góc A bằng , AB = a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng 6 điểm E, F, G, H, B, D cùng nằm trên một đường tròn. Xác định tâm và tính bán kính của đường tròn đó theo a.
Hướng Dẫn:

Gọi O là giao điểm của AC và BD ta có OB = OD
Do ABCD là hình thoi nên ta có:


Trên đây là nội dung và một số dạng bài tập cơ bản về chủ đề Tứ giác nội tiếp đường tròn. Hãy theo dõi ngay tại takis.vn để có thêm nhiều kiến thức mới và hay 3 môn Toán Anh Văn nhé!
Ý kiến bạn đọc
Bạn cần đăng nhập với tư cách là Thành viên chính thức để có thể bình luận
Những tin mới hơn
Những tin cũ hơn
Tin xem nhiều
-
 Hướng dẫn cách thay thế từ ngữ để bài văn trở nên đặc sắc, sinh động.
Hướng dẫn cách thay thế từ ngữ để bài văn trở nên đặc sắc, sinh động.
-
 Tổng hợp kiến thức Ngữ văn 6 - Bộ sách Kết nối tri thức (Bản chi tiết)
Tổng hợp kiến thức Ngữ văn 6 - Bộ sách Kết nối tri thức (Bản chi tiết)
-
 Học văn có ý nghĩa to lớn như thế nào?
Học văn có ý nghĩa to lớn như thế nào?
-
 Chủ đề học tập: Các đường đồng quy trong tam giác
Chủ đề học tập: Các đường đồng quy trong tam giác
-
 Cách ôn luyện từ vựng hiệu quả
Cách ôn luyện từ vựng hiệu quả
-
 Top 5 địa điểm cho thuê phòng hội thảo uy tín giá rẻ tại Hà Nội
Top 5 địa điểm cho thuê phòng hội thảo uy tín giá rẻ tại Hà Nội
-
 Tổng hợp một số chủ đề viết văn nghị luận thường hay gặp trong đề thi ( có bài tham khảo)
Tổng hợp một số chủ đề viết văn nghị luận thường hay gặp trong đề thi ( có bài tham khảo)
-
 3 lý do không nên phân biệt môn chính – môn phụ
3 lý do không nên phân biệt môn chính – môn phụ
-
 TOP địa điểm cho thuê phòng học giá rẻ tại Hà Nội
TOP địa điểm cho thuê phòng học giá rẻ tại Hà Nội
-
 Phân tích tác phẩm: Bếp lửa - Bằng Việt
Phân tích tác phẩm: Bếp lửa - Bằng Việt
